LambdaAPI2 design

LambdaAPI2 is another java-written implementation of pure lambda-calculus. Its aim is to support applications of pure lambda-calculus. LambdaAPI2 is based on constructs described in Compiling the Lambda-calculus into Interaction Combinators. For short, we will refer to that document as the LambdaCompiling document. The purpose of the present document is to explain how LambdaAPI2 represents the lambda-terms and realizes their reductions.

This document relates to version 1.0 of the LambdaAPI2 software.

• Lambda-term
• Lambda-net
• From term to net
• From net to term
• Optimizations

Lambda-term

Differently from LambdaAPI, LambdaAPI2 makes use of the usual definition (T ::= V|λV.T|TT) of lambda-terms. With LambdaAPI2, a lambda-term is either:

• a (free or bound) variable instance,
• the abstraction of a body lambda-term relatively to a set of zero or more variable instance(s) belonging to this body term,
• the application of a lambda-term (the function) to a lambda-term (the argument).

Each variable instance is unique. It is either free or bound to an abstraction, which contains this variable instance.

Access to lambda-terms is read-only. it is done through the java interfaces: Term, Variable, Abstraction, Application of the org/xmloperator/lambda2/term/model package.

Terms are instantiated using the VariableImpl class constructor and the buildAbstraction(...) and buildApplication(...) factory methods of the Term interface.

Term reducing is done through the TermReducer interface. It is not proposed a direct implementation of this interface but an indirect one using a combinators-based interaction net (interaction nets are known to be good engines for the lambda-calculus because their sharing characteristics).

Lambda-net

Lambda-nets are interaction nets that realize such a mapping with lambda-terms:

• A wire lambda-net maps to a variable instance.
• An abstraction lambda-net maps to an abstraction lambda-term.
• An application lambda-net maps to an application lambda-term.

Lambda-nets are made of cells (with ports), free ports and connections. By free port, we don't mean a port (of a cell) that is not connected but a port that belongs to no cell. We use free ports for closing the net, by connecting every port.

Free ports support the interaction net. There is a body support and zero or more free variable support(s). As an example, the simplest lambda-net, the wire lambda-net, is made of a body support connected to a free variable support. The entire lambda-net must be accessible through its body support. Disjoint parts of the net are garbaged.

The port, cell and lambda-net entities are represented by the java interfaces Port, Cell and LambdaNet of the org/xmloperator/lambda2/net/model package and their implementations PortImpl, CellImpl, LambdaNetImpl of the org/xmloperator/lambda2/net/impl package.

Nets are instantiated using the LambdaNetImpl class constructor and the buildAbstraction(...) and buildApplication(...) factory methods of the LambdaNet interface. The only difference with terms is replacing variable instances by free ports. The buildAbstraction(...) methods implements not only the Abstraction construct of LambdaCompiling but also the Eraser one and the Copy one.

From term to net

A lambda-term is translated into an interaction net for reducing.

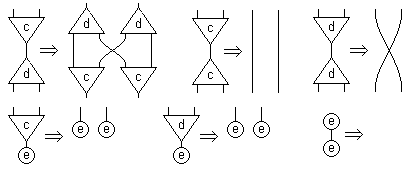
The used interaction system is composed of the three combinators of Lafont (eraser, duplicator, constructor) plus an abstractor and an applicator, which behave as multiplexors. Interactions rules for the combinators of Lafont are recalled here ("e" for eraser, "d" for duplicator, "c" for constructor):

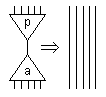
The abstractor (symbol "a") and the applicator (symbol "p") have an arity equal to five and interacts together by annihilation. Each one is erased by interacting with an eraser or duplicated by interacting with a duplicator. None interacts with a constructor neither with itself. Annihilation is shown here:

Specialized entities implement cells depending on their symbols:

• Eraser/EraserCellImpl implements the eraser,
• BinaryCell/BinaryCellImpl implements the constructor and the duplicator,
• PentaryMultiplexor/PentaryMultiplexorImpl implements the abstractor and the applicator.

The lambda-net is built at the image of the lambda-term it represents.

From net to term

After some reduction steps, we desire to read back the lambda-term a lambda-net represents. But this operation is not trivial because the lambda-net has no more the structure of a just built lambda-net. It needs to be decoded.

For decoding purpose, the interaction system is completed with an infinite set of indexed symbols, called decoders. A decoder (symbol "x") may have any arity and any index. The index represents a variable in the lambda-term. A decoder interacts only with the applicator, the duplicator or the eraser, as shown here:

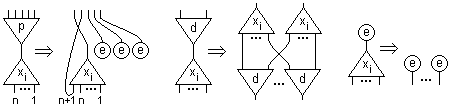
As an example, the net build from the lambda-term "xu", where the term "u" doesn't contain the variable "x", is decoded in the following way:

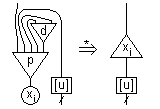
The process of reading back a closed (i.e. without free variable) term in normal form is the following:

• The lambda-net is reduced to interface normal form. Interface normal form of a lambda-net is characterized by the connection of its body support to a principal port. In order to obtain that interface normal form, the reductions are sequentialized and the selected active pair is always the principal one (this principal active pair is obtained, from the body support, by leaving each connected cell by its principal port, until being in face of another principal port). This reduction is said weak. The represented lambda-term is in head normal form.
• If the body cell (the cell connected (by its principal port) to the body support) is an abstractor then the represented term is an abstraction. Then action is made of applying (by building the application and reducing its active pair) a decoder with a zero arity and a new index (relatively to the stack of abstraction context).
• If the body cell is a decoder of arity n (n > 0) then the represented term has the form "xt1..tn", where "x" is a variable and "t1".."tn" are n terms. The index of the decoder gives the abstraction to which the variable is bound. Then, the same process is applied to the lambda-net(s) found behind the decoder.
• If the body cell is another cell then ... no, it's not possible! (demonstration left to the reader)

Optimizations

Optimizations occur at the term level, at the cell level and at the interaction level.

Optimizations at the term level:

• There are three different implementations of Abstraction, used depending on the count of bound variable(s). This save memory space.
• An implementation of Application includes a function exponent. This allows, for example, to code a Church numeral within a very small memory space. The function exponent is exploited at lambda-net reading back by recognizing sequences of linear decoder (arity equal to one) using the same index.

Optimization at the cell level:

• A cell and its principal port constitute one object instance. This save memory space.

Optimization at the interaction level:

• Commutating a constructor and a duplicator (which is a relatively costly operation) can be avoid if the auxiliary ports of the duplicator are both connected to the principal port of a constructor. The BinaryCell implementation allows to transmute a constructor into a duplicator. This save time.

Nothing special is made about garbage collection.